How I Learned to Love Math as a Language Specialist (Part 3/3)

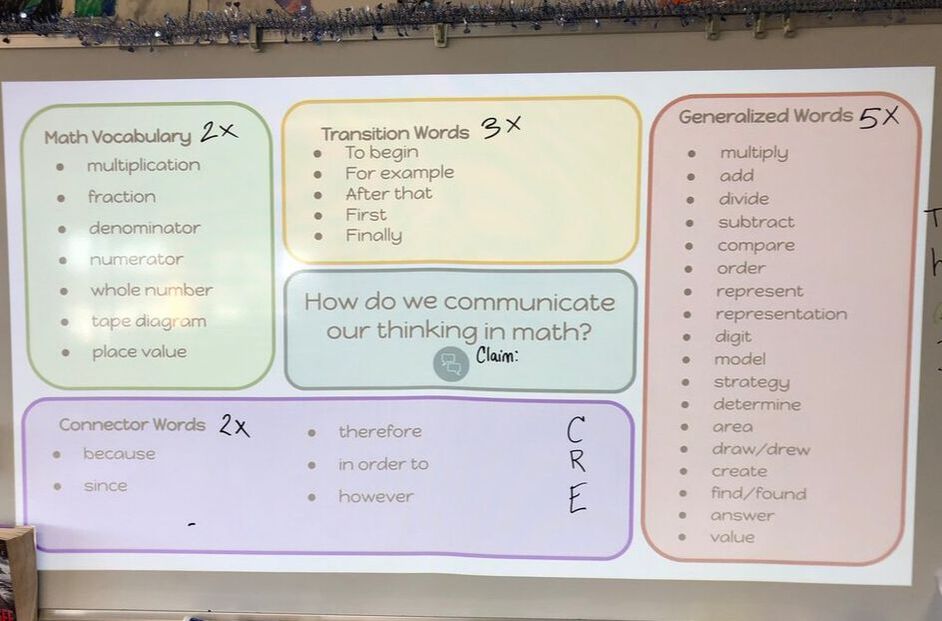
Thanks for sticking with me this far in this series of blog posts.  In case you missed it, Part 1 and Part 2 can be found here. If you have made it this far, you are probably here for the strategies.  You want to actually see it; what does co-teaching or collaborative content and language integrated learning look like in a multilingual math classroom?

To begin, the goal of a language in a math classroom has to be building students to the discourse of mathematics. Discourse is about sharing their thinking, findings, critiques, and analysis. The discourse is about thinking flexibly and making meaning together as a community of young mathematicians.  This means that as an MLL specialist in the math classroom I am creating the conditions for sharing, in writing or speaking.

However, we don't start at discourse right away within a unit. When I am co-designing at the curricular level, I am always thinking of the vocabulary and grammar that are the brick and mortar to building discourse. Furthermore, I design for oracy and written practice. Finally, I think about progressively using different strategies with exposure and practice in mind, as we move towards mastery; which is of course-the mathmatical discourse.

student examining the class' Knowledge Rating Scale

A straight forward vocabulary strategy I often begin with is the KRS chart, or the knowledge rating scale. In the past, I have had large class KRS charts, or personal copies for each student. It can be a straight forward table with color coding, or it can be layered with visual scaffolding to make it more accessible to a range of language proficiencies. An early goal of this strategy is to expose students to prioritized vocabulary in the content area and activate background knowledge. It also serves as a formative assessment tool for teachers. Additionally this vocabulary strategy is builds students self-assessment literacy. It is a reflection tool. It can be revisited throughout the course of a unit in math. We take it out every time we engage in language work together in class. The students begin to see their vocabulary knowledge grow, sometimes from direct instruction from me and sometimes from their conceptual/skill development with their math teachers.

---

a screenshot of a slide for after reflection on the KRS chart

Of course we can't stop there. By activating prior knowledge and engaging in regular reflection we have created the conditions for interdependence.  Initially students have different degrees of understanding of the vocabulary. This offers an authentic opportunity for oracy work and to get kids talking. This is an early level of mathmatical discourse. It also offers an authentic opportunity for translanguaging. Students that understand a vocabulary word or concept in another language, can teach their peers that way too. Creating the conditions for interdependence, helps build our class as a community of learners, develop collaboration skills, and facilitates talking to each other.  Recently, I find myself folding in our schools' different dispositions/ competencies /learner attributes as a reflection tool after kids have collaborated to make meaning.

---

information gap activity

an example of what the information gap cards might look like

Another goal of mathmatical discourse is to help students engage in mathmatical problem solving together. One speaking/listening/problem solving strategy that kids have enjoyed is the information gap. I learned about this one in a course I took with Jeff Zwiers.  To summarize it briefly, one partner has a numberless word problem on a card. The other partner has the numbers with labels needed to solve the word problem. Partner A (who has the word problem) has to ask a question that asks for the number of something that will enable them to begin solving the problem. Partner B has to ask "why do you need to know that?"  Partner A then has to justify their reasoning based on the problem. Not only is this strategy is promoting speaking and listening for our learners, it is nurturing mathmatical reasoning and justification.  Justification of course offers an opportunity to push into the language function and grammatical features.  The mortar of our language.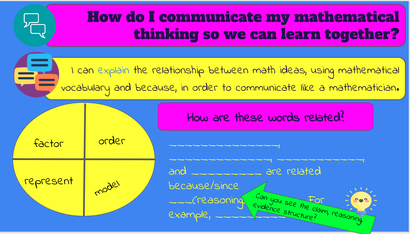

example of concept circle partnered with sentence starters

There are a lot of great vocabulary strategies out there to help students make meaning of a word. I regularly use variations of a bilingual frayer square or Quizlet. Yet, I don't want to stay at the "define and understand" level of vocabulary. I want them to continue to build connections and work in the justification space. One strategy I return to again and again, is the concept circle. Bonus-it's extremely low prep. Don't let that screenshot of a slide above fool you, sometimes I draw a circle in quadrants with four words in each section on the white board.  I select 4 words. I ask a question: how are these words related? Students then have to make a claim and justify.  Once again, it is a vocabulary strategy, a language function opportunity, and a discourse strategy. Sometimes I will select 4 words and pose the question: which word does not belong? And again students will have to justify their claim. Oftentimes students have widely different thoughts and answers.  Once again, we have created the conditions for interdependence, where we can learn from each other and grow our flexibility as mathematicians. I then partner the concept circle with a verbal interaction strategy (an example like the Kagen engagement strategies like Mix-Pair-Discuss) to get the kids talking, sharing, and learning from each other.

---

concept sort

Another low prep strategy I love is the concept sort. I print out our vocabulary words on a sheet. I make the kids cut them out. I form groups of 2-3. And I pose the question: how are these words connected? That's it. Sometimes we use yarn to make the connections. Sometimes we use anchor chart paper, glue, and markers. Next I essentially, sit back and listen. Kids will argue, make claims, rework 

---

their claims. Kids might get stuck and then with the right coaching question, the will get unstuck. This is language discourse at its finest, using mathmatical vocabulary. Finally, we will do a Gallery Walk and see the different ways groups organized their connections. Kids will be invited to ask questions or revise their thinking. It is always noisy. It is always fascinating.

a color coded language anchor chart

a color coded snapshot from an explanation from a young student's math notebook.

Finally as we move through the unit, and have learned different vocabulary words while my co-teachers have taught the different concepts, I like to bring out the above chart. I have populated it with mathmatical  words we have learned about and different connector words. After that we

---

examine a math problem the students have recently solved with my coteacher. From there, we begin to co-construct a list of everyday words (Tier 2 vocabulary) that has multiple meanings, that we would need to explain our recently solved math problem. We are putting it all together.

These are just some of my favorite language strategies I employ in my co-taught classrooms from my instructional toolbox. I love trying out new ones or iterating on familiar ones. It's never about which kids are on my "caseload" or which kids are "struggling". It's about the joy of making meaning with language together-for all students. As an MLL teacher and someone who is in recovery from math anxiety, I have found my voice and my place in the mathematics classroom. And in all honesty, I've not just found my place, I've learned to love math.